How to solve cartonization for e-commerce groceries using Machine Learning
Logistics is the heart of e-commerce. Most of the problems that you need to solve when you are working on creating an e-commerce business…
Logistics is the heart of e-commerce. Most of the problems that you need to solve when you are working on creating an e-commerce business end-to-end are related with being able to prepare orders and deliver the purchase at customer’s home.
One of those problems is cartonization, which means to be able to know in advance how many crates will be needed to prepare and pack the customer’s order. This problem is even more important for us, in Mercadona Tech, since one order has in average from 40 to 50 products and from 60 to 70 items.
At the beginning of the project with started to use a very basic heuristic, since we didn’t have enough data to learn how to carry out this task in a more efficient way, but after several months gathering data we realized that we had enough information to move forward with a better approach applying some very basic Machine Learning techniques.
As I mentioned above, cartonization is the process of evaluating the items included in an order to determine the number and size of each shipping carton needed. The weight, height, length and width of each item is used along with basic mathematics to determine the best way to pack each carton. In our case, we reduced cartonization to getting the number of crates that will be needed during the picking process for every order.
Given that we needed to predict the number of crates, the problem was modeled as a regression problem, since we wanted to predict a continuous value.
Correlation Analysis
The easiest way to find high quality features is using Correlation Feature Selection (CFS) where a good feature highly correlated with the label that we want to predict and yet uncorrelated to each other feature of the model. When we have several features CFS allow us to find the best set of features that minimize our Loss function.
For this exercise, we studied how correlates the total volume of the orders with the number of crates prepared by the pickers in the warehouse.
Input Variables (Feature):
total_volume: The total volume of each order which is the sum of the volume of all the products included in the order.
Output Variable (Label):
Number of crates: number of crates prepared by the pickers in the warehouse given an order during the last 6 months.
Correlation analysis with Pandas is very straithgforward, once we had the dataframe ready we run a basic correlation analysis getting a correlation heatmap:
… and the correlation values
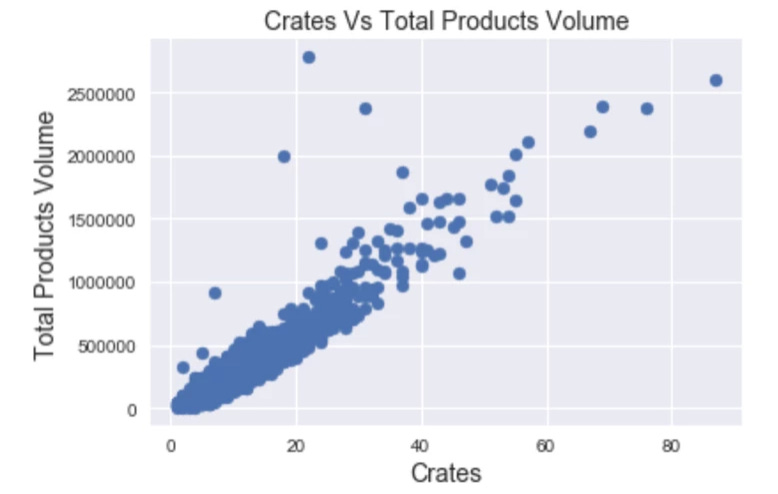
Having a correlation value of 0.93 was a very good starting point. However, drawing a scatter chart was also a good way to figure out how good the correlation was, since a high correlation could hide a trap because the nature of the outliers or the data distribution.
Taking this issue in mind, we analysed how our to variables correlates when graphed.
Well, everything looks great actually, a few outliers could be removed but we had tones of data points keeping a consistent behaviour, which confirms that the total order volume was a good predictor of the number of crates.
Prepare Features
Once we had found a good predictor was time to prepared the data to be ingested by the learning algorithms. Fist step was to extract a dataframe with the selected features and an array with the corresponding labels.
Training, Test and Validation Sets
Splitting the dataset was the next step. We created three partitions of the data set:
Training set — a subset to train a model.
Test set — a subset to test the model.
Validation set — a subset to validate the Test set results and reduce your chances of overfitting
Getting this task done with scikit-learn was very easy:
Features scaling
Feature scaling is a method used to standardize the range of independent variables or features of data. Most of ML algorithms are very sensitive to feature scaling, especially Stochastic Gradient Descent, so we needed to apply some normalization methods. Without normalization, our training could blow up with NaNs if the gradient update was too large.
In every model you create is always highly recommended to scale the data and figure out what is the impact of scaling your features in the model performance.
There are several feature scaling techniques, where min-max normalization is the simplest one.
Scikit-learn allows you to do this in a ver easy way:
Learning Algorithm: Stochastic Gradient Descent Regressor
Finally we were ready to run our learning algorithm. We applied a Linear Model to predict the number of crates given an order. Linear models describe a continuous response variable as a function of one or more predictor variables. They can help us to understand and predict the behavior of complex systems or analyze experimental data. Linear regression is a statistical method used to create a linear model.
Linear Regression general formula
where
y is the value we are trying to predict
m is the slope of the line
x is the value of the input feature
b is the y-intercept
Linear Regression formula for Machine Learning
where
y’ is the value we are trying to predict. Number of crates.
b is the bias (the y-intercept), sometimes referred to as w_0
w_1 is the weight of the feature 1. Weight is the same concept as the “slope” m in the traditional equation of a line
x_1 is a feature, a known input. Total Volume of the order
Running linear regressors using SGD with scikit-learn was very easy:
Benchmarking
We already had an algorithm up and running for cartonization, based on the order volume, so we made the decision to use this formula as a kind of naive predictor of the number of crates to set up a benchmark:
Evaluation
Once we got the model trained and the benchmark, we needed to evaluate the performance of our learning algorithm to compare the results with the heuristic that we were using as a benchmark. The metric selected were Mean Absolute Error (MAE), Root Mean Squared Error (RMSE) and Mean Squared Error (MSE).
Running this evaluation metrics using scikit learn was quite simple:
The evaluation metrics for the benchmark algorithm return the following results:
Mean Absolute Error: 2.44 crates.
Root Mean Squared Error: 2.82 crates
Mean Squared Error: 7.96
Plotting the prediction and actual data we get the following plot:
So, now we knew where the bar was and therefore, we were able to figure out if our ML based approach would be worthwhile or not.
For the linear regressor we got the following results:
Mean Absolute Error: 1.16 crates.
Root Mean Squared Error: 1.66 crates
Mean Squared Error: 2.76
We also can also plot how well match real values with the prediction
Plotting the prediction and actual data we get the following plot:
Results looks great!, since the error was much lower using the ML approach compare with the benchmark, which means that we were able to reduce the error of getting more crates than needed to prepare a given order.